Lorsque l’on parle de modèle computationnel, et de son implémentation, on pense évidemment à des modèles informatiques. Pourtant avant l’avènement de l’informatique, plusieurs modèles ont été conçus avec des dispositifs physiques ou hydrauliques. La première marchine a vu le jour dans l’antiquité avec la machine d’Anticythère. Jusqu’aux années 1980, les marées étaient prédites avec des poulies, et les transferts thermiques simulés en URSS avec des intégrateurs à eau ! Ces simulateurs physiques sont aujourd’hui utilisés à fin pédagogique, mais se sont frayé un chemin jusqu’à la pop culture.
Un modèle computationnel n’est pas toujours informatique
Un modèle computationnel suppose de dérouler un algorithme, des calculs. Il est donc évident que la plupart du temps, ce type de modèle est exécuté avec un ordinateur. Pourtant il est possible de réaliser des calculs sans ordinateur.
Un exemple célèbre de modèle d’automate cellulaire, le modèle de séggrégation de Schelling, a été initiallement prototypé par son auteur en utilisant une grande feuille de papier quadrillée représentant la structure 2D du monde, et des pièces cuivrées ou argentées (dimes and pennies).
A l’opposé des ordinateurs qui calculent à base de digits (de 0 et 1), plusieurs ordinateurs analogiques ont été conçus qui utilisent d’autres phénomènes physiques pour implémenter un calcul.
Simuler à la main
Certains calculs, ou règles de simulation, sont assez simples pour être exécutée manuellement.
Un exemple célèbre de modèle d’automate cellulaire, le modèle de séggrégation de Schelling, a été initiallement prototypé par son auteur en utilisant une grande feuille de papier quadrillée représentant la structure 2D du monde, et des pièces cuivrées ou argentées (dimes and pennies).
Engrenages et horlogerie
Plusieurs modèles ont été implémentés à l’aide de mécanismes à base d’engrenages et autres dispositifs apparentés à l’horlogerie.



La Machine d’Anticythère est le premier calculateur à engrenage connu. Fabriquée dans l’antiquité, avant -80 avant JC, cette machine actionnée par une manivelle décrivait le mouvement des planètes visibles. Plus tard d’autres calculateurs mécaniques de positions du soleil, tels que l’Astrolabe conçu en grèce, seront conçus.
La « Machine à prévoir les marées » conçue par William Thomson en 1872 est un dispositif mécanique qui calcule les heures et amplitudes des marées, en tant compte des positions relatives de la Terre, de la Lune et du Soleil, et d’autres paramètres locaux. Ces machines ont été améliorées progressivement et utilisées dans plusieurs pays pour calculer les prévisions officielles de marées. Pendant la seconde guerre mondiale, l’Allemagne conduit un projet stratégique visant à créer sa propre machine pour disposer des prévisions nécessaires à la bataille de l’Atlantique. Ces machines seront remplacées à partir de 1960 et 70 par des ordinateurs.
Enrico Fermi a inventé le FERMIAC pour modéliser des flux de neutrons. Cette machine prend en paramètre une distribution initiale de neutrons, puis procède à la simulation aléatoire de neutrons lents et rapides, en prédisant les mécanismes de collisions, évasions et fissions.
De nombreux principes mécaniques ont été utilisés pour réaliser des calculs de plus en plus complexes. Les intégrateurs à billes et disques inventés par James Thomson par exemple permettent l’intégration de deux signaux, et seront utilisés par William Thomson pour créer son analyseur d’harmoniques. L’analyseur d’harmoniques sera mis en service en 1878 pour analyser les enregistrements des changements quotidens de température et pression atmosphérique.
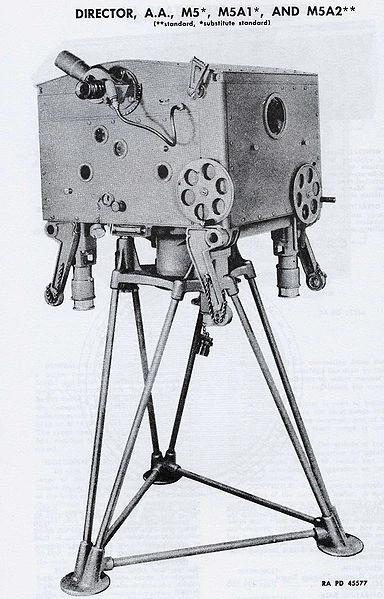

De nombreux engins ont été conçus pendant la seconde guerre mondiale pour améliorer le ciblage dans l’armement. C’est le cas du prédicteur Kerrison qui aide un tireur de DCA à viser un avion rapide en prédisant sa position prochaine. Ce prédicteur simule le mouvement probable à l’aide de composants mécaniques.
De façon plus générale, l’intégrateur à billes et disques, peut être considéré comme un analyseur différentiel (voir l’article en anglais, plus fournit: differential analyzer). Ces analyseurs différentiels seront également intégrés dans des calculateurs analogiques électroniques (voir plus bas). Ils seront utilisés pour de nombreuses applications, comme la conception de bombes rebondissantes pour détruire des barrages hydrauliques ennemis, ou pour étudier l’érosion des cours d’eau.
Simuler avec l’hydraulique
On peut utiliser l’eau (ou autre fluide) dans un réseau de tuyaux et réservoirs; la physique des flux d’eau peut être une analogie valable de flux d’une autre nature, tels que des flux monétaires.
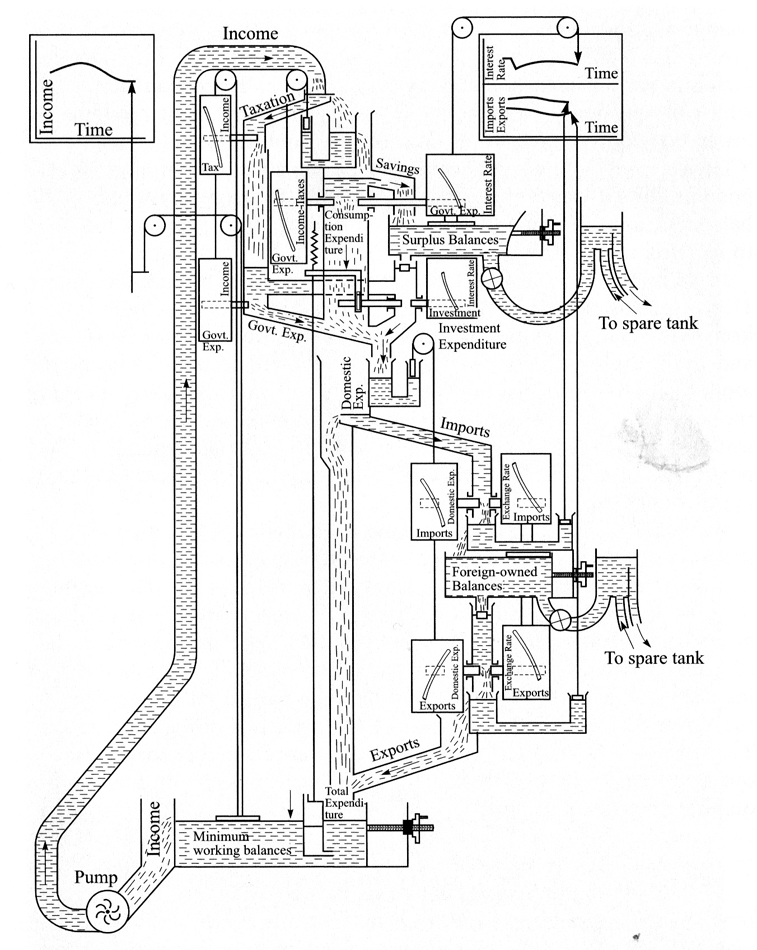


Le modèle économique MONIAC (Monetary National Income Analogue Computer) utilise un dispositif hydraulique pour représenter des flux monétaires entre compartiments. Ce modèle computationnel analogique a été proposé par William Phillips en 1951, afin d’enseigner l’économie. Le MONIAC a inspiré dans la culture populaire le simulateur « le Gloupier » dans le roman satirique « Monnayé » de Terry Pratchett.
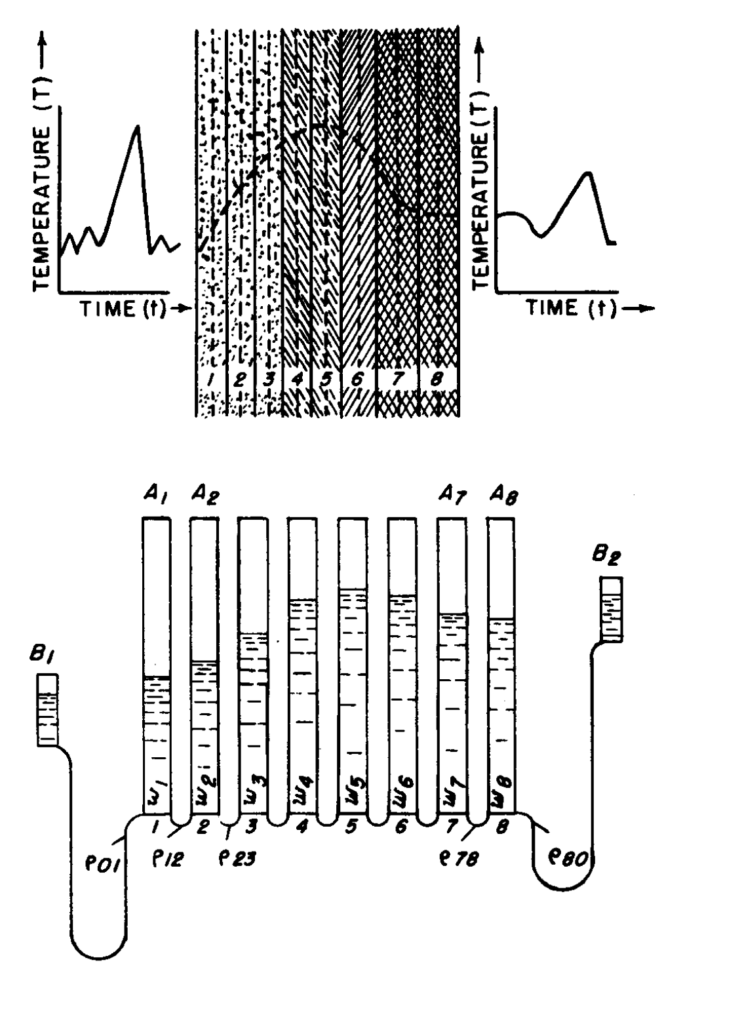

Un calculateur à eau soviétique, l’intégrateur hydraulique de Loukianov, a été conçu par Vladimir Sergueïevitch Loukianov pour modéliser des phénomènes thermiques dans des matériaux, et étudier la fissuration du béton pour la limiter. La simulation repose sur une analogie entre les phénomènes réels et la dynamique hydraulique: différents récipients se déversent les uns dans les autres via des tubes, au même rythme que la température se propage entre des mailles d’une paroi. Ce modèle générique a été appliqué utilisé pour la conception de plusieurs ouvrages: canal de Karakoum, la ligne principale Baïkal-Amour, centrale hydroélectrique de Saratov. Son usage a été étendu à d’autres matériaux, avec d’autres applications en métallurgie, géologie, ou science des fusées. Voir notamment cette page en russe.
Si l’hydraulique n’est plus utilisée aujourd’hui pour réaliser des calculs, l’analogie générale entre physique des fluides et d’autres phénomènes est toujours considérée comme valide dans certains contextes. C’est ainsi que le traffic routier, ou des flux de piétons, sont souvent modélisés sur la base d’analogies avec des fluides.
Calculateurs électroniques analogiques
des calculateurs spécifiques…
Des calculateurs analogiques ont été développés pour modéliser et simuler des phénomènes spécifiques (au sens où on ne pouvait pas utiliser un calculateur pour modéliser autre chose que le système prévu lors de sa conception, contrairement à un ordinateur contemporain que l’on peut programmer pour étudier n’importe quel problème). Dans de tels calculateurs, des circuits électroniques décrivent le système que l’on étudie.



Le calculateur de submersion de Shizuo Ishiguro, le « Ishiguro Storm Surge Computer« , a été développé vers 1956 pour simuler les risques de submersion marine au Japon. Les calculs sont réalisés de façon électrique en utilisant une analogie entre courant électrique et hydraulique: chaque point d’une grille de 50 sur 50 connecteurs représente une maille spatiale. La tension représente la hauteur d’eau, l’intensité représente le débit d’eau. Les circuits électriques qui inteconnectent les points de la grille simulent les propagations de courants de proche en proche, et intègrent des calculs tels que les forces de marée et les forces de Coriolis.
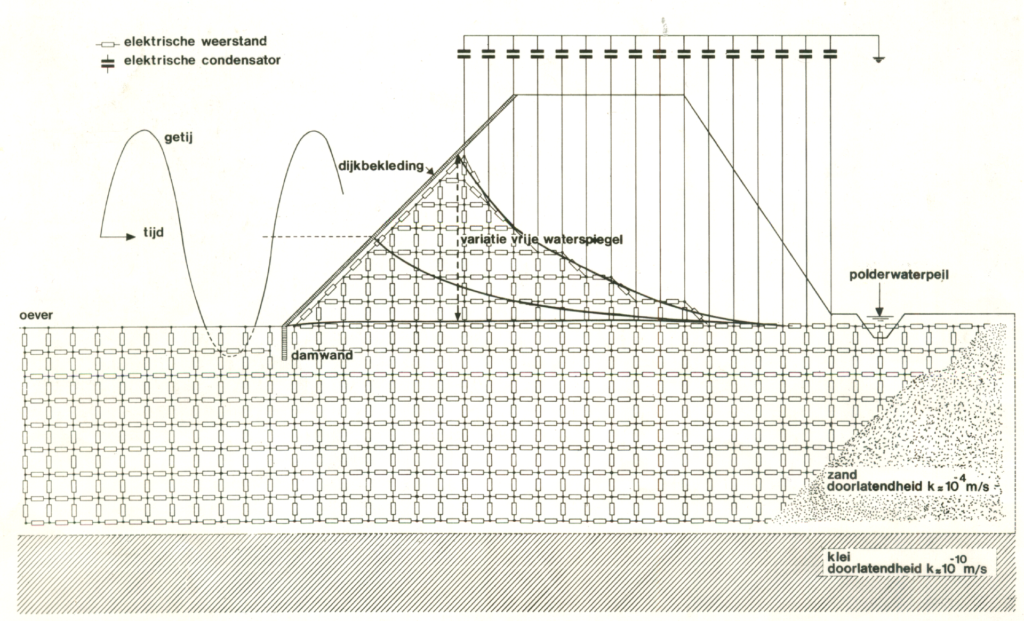

Le calculateur Néerlandais ELNAG a été conçu pour étudier les niveaux d’eau souterraine et sécuriser les digues. Le modèle est constitué d’un réseau de résistances et condensateurs. Chaque condensateur permet de représenter l’accumulation progressive d’eau sur une maille de terrain. Les résistances modélisent les transferts progressifs d’eau entre mailles.
…puis des calculateurs analogiques génériques
Avec le temps, des calculateurs analogiques génériques ont été développés vers les années 1950-80. Contrairement aux exemples cités plus haut, ils disposent de circuits électroniques génériques (tubes à vide, résistances, condensateurs, inductances…) qui peuvent réaliser des opérations élémentaires tels que les additions, les soustractions, l’intégration, la différentiation. Par contre, à cause des principes physiques utilisés, ils ne peuvent pas réaliser certains calculs comme les divisions. On programme ces ordinateurs par cablage des composants (ce que qui est la façon de les programmer pour traiter un problème donné). Le résultat est lu en temps réel sur un dispositif de résultat, généralement un écran d’oscilloscope qu’il faut savoir interpréter.
De tels calculateurs analogiques génériques ont été développés commercialement en très petite série dans plusieurs pays. Aux USA, les calculateurs de l’américains Electronic Associates Inc. ont été notamment utilisés pour l’étude de sondes spatiales. En France, deux sociétés produisent des calculateurs1: la SEA (Société d’Electronique et d’Automatisme) et les Laboratoires Dervaux. Les calculateurs analogiques électroniques SEA OME P2, et ses variantes, seront utilisés en batterie par la société SNECMA (l’ancêtre de Safran) pour mettre au point les commandes de vol du Concorde. La Pologne conçoit et utilise son calculateur ELWAT. Au Japon, la société HITACHI produit des calculateurs analogiques; en Allemagne, la société TELEFUNKEN, etc.
Ces ordinateurs analogiques ont plus tard été supplantés par les ordinateurs numériques que nous connaissons aujourd’hui, qui fonctionnent selon le principe de machine de Turing: la machine peut lire des instructions depuis une zone de programme, des données, et réaliser des opérations élémentaires dans une mémoire de travail.
Pour en savoir plus sur les calculateurs numériques, une belle explication sur cette page de Interstices, cette page d’un collectionneur d’ordinateurs analogiques.
D’autres simulations physiques
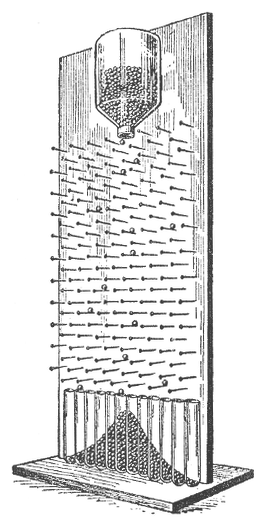
La Planche de Galton (en anglais: « quincunx ») est une planche en bois sur laquelle sont plantés des clous en quinconce. Chaque bille qui tombe du réservoir, au centre de la planche, tombe sur un clou, et s’oriente aléatoirement à gauche à droite. A la rangée suivante, la bille tombe sur un autre clou, et à gauche ou à droite, etc. Cela met en pratique une loi de probabilité binomiale. En bas de la planche, des réceptacles reçoivent les billes tombées dans différents compartiments. En faisant tomber plusieurs billes, on constate que les billes tendent à tomber vers le centre, et ont une probablité de plus en plus faible à tomber plus loin du centre. Quand on fait tomber beaucoup de billes, les réceptacles font apparaître une courbe de Gauss. Voir l’excellente explication sur le site des sorciers de Salem.
Pourquoi simuler ? Reprendre le véritable système en plus petit
La simulation numérique décrit l’état du système sous forme de données représentées de façon numérique. Mais il est possible de simuler en utilisant le monde réel, en le faisant à une plus petite échelle (une maquette d’un bâtiment au lieu d’un bâtiment, un tronçon de route au lieu d’une vraie route, 50 personnes au lieu de 50000…) et dans des conditions plus contrôlées.
Il arrive que l’on utilise le monde réel pour modéliser et simuler un phénomène « en plus petit » et de façon plus contrôlée. C’est le cas de la simulation de traffic routier présenté dans la vidéo ci-dessus, ou de l’évacation de foule, ou encore de la simulation de tremblements de terre.

Pour aller plus loin
Cette page sur le calcul avant les ordinateurs: https://www.scientific-computing.com/feature/revealed-grace-mechanism-computing-after-babbage
- page « Calculateur analogique SEA OME P2 » sur le site de l’Association pour un conservatoire de l’informatique et de la télématique: https://www.aconit.org/spip/spip.php?article244 ↩︎

Chercheur, modélisation de systèmes énergétiques pour l’aide à la décision






